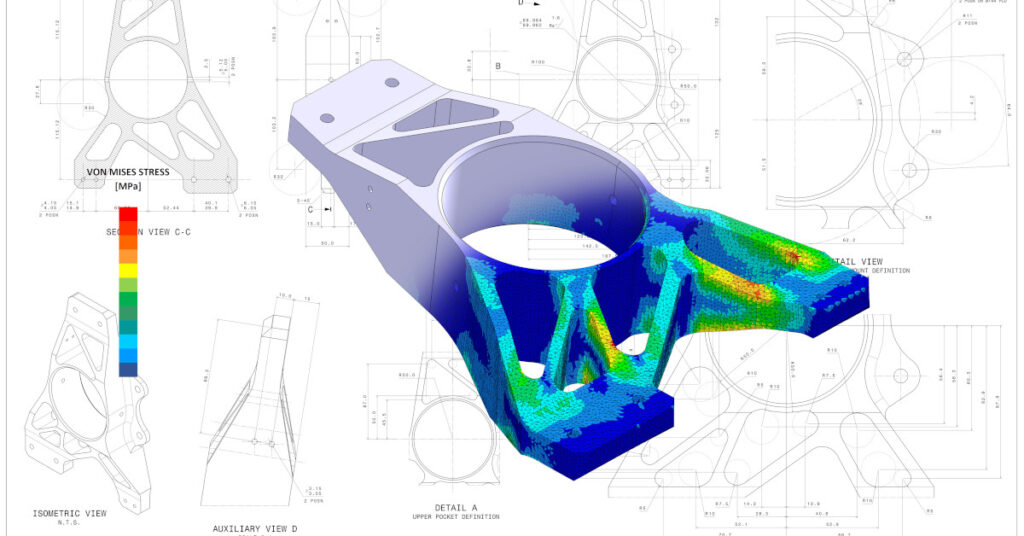
Mas afinal, o que é Análise por Elementos Finitos? Para que serve? E quais são os passos realizados?
Neste artigo, apresentaremos o conceito, as etapas necessárias e a aplicação do método.
O que é o Método dos Elementos Finitos (MEF)?
O método dos elementos finitos (MEF) ou a Análise por Elementos Finitos (FEA) é uma técnica amplamente utilizada em engenharia e física para resolver problemas complexos de forma eficiente e precisa. Em primeiro lugar, divide a geometria do sistema em pequenos elementos finitos, que são modelados como equações matemáticas para representar o comportamento do material dentro deles. Em seguida, um modelo completo do sistema forma-se pelas equações combinadas.
De maneira geral, o MEF possibilita resultados para indicar a durabilidade do componente, verificar pontos de concentração de tensão, analisar o comportamento da estrutura sob carregamento e permitir a otimização de peças antes da fabricação.
Quais são as etapas para a Análise por Elementos Finitos?
1. Criar modelo CAD do sistema sob análise
Um modelo CAD (Desenho Auxiliado por Computador) é a representação em 3D da peça ou sistema analisado. A importância desse modelo na análise por elementos finitos está em permitir aos engenheiros avaliar diferentes cenários de projeto de forma virtual, antes de criar um protótipo físico. Isso reduz o tempo e o custo de desenvolvimento de novos produtos e sistemas, além de permitir que os projetistas possam testar diferentes opções de design para avaliar a melhor solução para um problema específico.
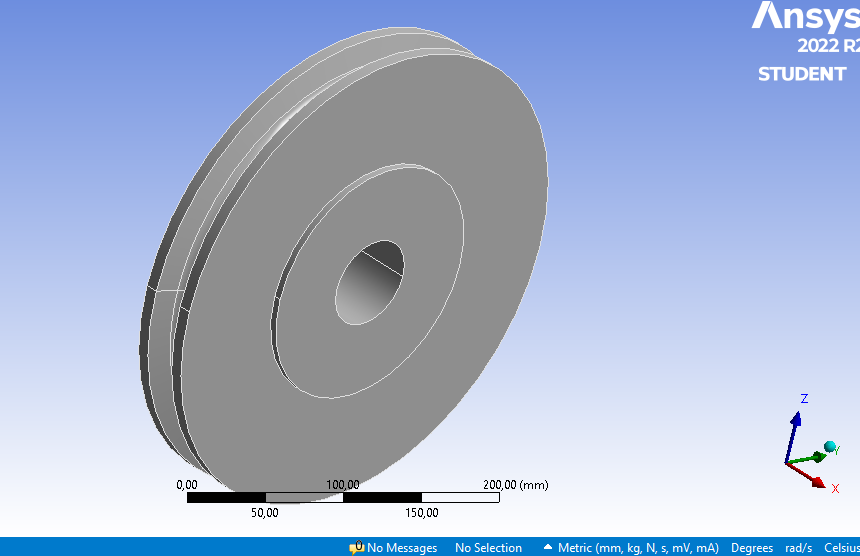
2. Fazer a malha
A malha é uma rede de elementos finitos usada para discriminar um objeto ou sistema físico em segmentos para análise matemática. A importância da malha está relacionada à maneira como os elementos finitos são distribuídos sobre a geometria do objeto ou sistema. Nesse sentido, a precisão da análise pode ser comprometida quando a malha é muito grossa, ou seja, quando os elementos são muito grandes em relação ao tamanho do objeto. Por outro lado, a análise torna-se muito complexa e computacionalmente intensiva quando a malha é muito refinada, ou seja, quando os elementos são muito pequenos em relação ao tamanho do objeto.
3. Definir as propriedades do material
As propriedades do material influenciam diretamente no comportamento mecânico da peça, como módulo de elasticidade, coeficiente de Poisson e resistência à tração. Por isso, é importante conhecer as propriedades mecânicas do material. Dessa maneira, é feita anteriormente análises nos materiais. Uma definição inadequada pode levar a resultados imprecisos e erros na análise por elementos finitos.

4. Definir as cargas e os contornos
Cargas e condições de contorno são elementos fundamentais em uma análise por elementos finitos. As cargas referem-se às forças ou momentos externos aplicados à peça e que podem afetar sua deformação e tensão. Por exemplo, as cargas podem incluir forças gravitacionais, cargas térmicas, cargas elétricas e cargas mecânicas. As condições de contorno, por outro lado, referem-se às restrições que limitam o movimento da peça. Essas restrições podem ser físicas ou podem ser impostas artificialmente como parte da análise, como a restrição de deslocamento em determinadas áreas.
É importante definir corretamente as cargas e condições de contorno para obter uma análise precisa e confiável. Uma definição incompleta pode levar a resultados imprecisos e erros na análise, o que pode afetar as decisões relacionadas ao projeto ou processo de produção da peça. Portanto, a definição correta das cargas e condições de contorno é um elemento fundamental para a análise por elementos finitos.
De maneira ilustrativa, segue um exemplo da Ensus de uma análise de elementos finitos com todas as etapas realizadas.
Quais são as aplicações do Método dos Elementos Finitos?
Em resumo, a principal vantagem do método dos elementos finitos encontra-se na solução de problemas complexos, os quais seriam difíceis ou impossíveis de resolver de outra forma. O MEF permite que o modelo matemático resolva-se em partes menores, ao dividir a geometria em pequenos elementos. Além disso, a precisão do método ajusta-se facilmente, sendo uma ferramenta flexível e versátil para uma ampla variedade de aplicações.
Por fim, as aplicações do método dos elementos finitos são diversas e incluem o projeto e análise de estruturas, como pontes, edifícios e componentes de aeronaves e veículos. Assim também, usa-se para simular o fluxo de fluidos em dutos e canais, analisar a transferência de calor, eletromagnetismo, acústica e outras áreas da física aplicada. Além disso, é uma técnica muito útil para engenheiros e cientistas, já que permite a resolução de problemas complexos de forma mais rápida e econômica do que os métodos analíticos tradicionais.
Quer otimizar seu equipamento antes de fabricá-lo?
A Solidus Júnior oferece serviços de modelagem 3D e Análise por Elementos Finitos para fornecer ao seu projeto maior segurança e qualidade.
Se quiser saber mais como esse método pode ser a solução que procura, fale agora com um especialista da Solidus.